Saneamento Ambiental e Autodepuração de Rios

1 Contextualização do Tema

A maioria das cidades é construída próxima de rios, lagos ou estuários porque esses ambientes naturais contribuem com a sobrevivência das pessoas. Mas, estes ecossistemas aquáticos também são utilizados como esgotos naturais e gratuitos. Seria desejável que as pessoas percebessem como medir a necessidade de afastar, acondicionar adequadamente e descartar corretamente seus resíduos em rios e mares. Porém, isso depende de interações entre gestores públicos, especialistas, atores da sociedade civil, atores econômicos, mídias e políticos. Há um falso conforto por causa desses ecossistemas possuírem águas correntes (rios e riachos), que possibilita o descarte indesejável dos resíduos humanos. No Brasil, esse comodismo compromete a condição sanitária e piora a estética urbana de um grande número de municípios.

Em qualquer ecossistema a maior diferença entre os seres humanos e os outros seres vivos é que os humanos são imprevisíveis. Todas as outras criaturas agem de acordo com regras de sobrevivência bem estabelecidas. Por isso, os humanos necessitam de uma escolaridade básica rigorosa que possa promover uma capacitação para associar os conteúdos das disciplinas ensinadas com uma sobrevivência ética, sanitária e coletiva. Essa escolaridade deve acontecer desde a infância, para quando chegar na fase adulta não ficar sozinha com o compromisso de adquirir o raciocínio crítico da ligação entre ciência e vida. Deixar uma criança crescer sem envolvê-la em temas coletivos como saneamento e saúde pública corre-se o risco de que em um futuro próximo sua atitude fique mais egocêntrica do que ecocêntrica. O individualismo é inimigo da organização de ecossistemas. Seria viável que a promoção da educação em saúde ambiental fizesse parte do conteúdo básico de todo currículo escolar fundamental de forma universal, livre e gratuito, como questão de interesse para a sobrevivência da espécie humana. Isso permitiria contribuir com a prevenção de doenças, com a redução da propagação de vírus, fungos e parasitas, otimizaria o controle de epidemias e diminuiria a transmissão de agentes contagiosos por vetores. Essa promoção escolarizada deveria acontecer de forma contextualizada com o local de moradia das pessoas. A falta desta promoção destrói, em qualquer país, não apenas o seu sistema econômico privado ou público, mas também sua infraestrutura urbana ou rural.

Deve-se considerar que dentro de um ecossistema aquático existem três grupos de seres vivos - os produtores, os consumidores e os decompositores. Esses organismos interagem continuamente entre si. Essas interações são consequências direta ou indireta das suas relações com a radiação solar, com a fotossíntese e com os diversos nutrientes encontrados na Natureza. As interconexões são descritas nos ciclos biogeoquímicos da biosfera. Por exemplo, o nitrogênio é formador das proteínas, como também o fósforo, o potássio, o carbono, o enxofre, o ferro, o oxigênio e muitos outros elementos já conhecidos na Tabela Periódica. O fósforo e o potássio estão presentes em formações minerais (solos e rochas), o nitrogênio pode ser fixado por bactérias ou gerado por descargas elétricas atmosféricas. A sobrevivência dos seres vivos depende de todos esses elementos (nutrientes) existirem em quantidades corretas e oriundas de fontes naturais para o delicado equilíbrio dos ecossistemas. Inclusive, na presença desses quantitativos em alimentos utilizados pelos humanos. Após os seres vivos utilizarem esses nutrientes eles têm de ser devolvidos ao meio ambiente, mesmo que de outra forma, para entrar na cadeia alimentar de todos novamente. Qualquer excesso, ou carência, ou incrementos artificiais nesses elementos pode ser fatal para a sobrevivência dos humanos, ou das outras espécies.

Em ecossistemas aquáticos os seres produtores são assim chamados por produzirem seus próprios alimentos nos processos de fotossíntese, por exemplo, as algas. Os organismos consumidores são assim determinados pois necessitam, direta ou indiretamente, ingerirem os nutrientes fabricados pelos seres fotossintetizantes (produtores). A devolução ao meio ambiente ocorre por intermédio dos seres decompositores, que decompõem a matéria orgânica (resíduos excretados ou corpos mortos de outros seres vivos). Nesse processo, eles oxidam a matéria orgânica como reciclagem natural formando novos nutrientes. Esses seres decompositores são microrganismos que vivem no lodo do fundo da água, por exemplo, as bactérias.

2 Mecanismos bioquímicos, autodepuração e influência humana em ecossistemas de águas correntes

Quando a matéria orgânica biodegradável é despejada no meio aquático, por exemplo, via efluente de esgoto, ela é digerida pelos decompositores por mecanismos bioquímicos, mas as não biodegradáveis são mortais para os seres vivos. Os decompositores chamados aeróbios respiram o oxigênio dissolvido na água para oxidar os materiais orgânicos em suspensão na água limpa e competem com os organismos dos outros dois grupos, produtores e consumidores. Conforme a matéria orgânica (elementos nutrientes), continua a entrar por despejo de esgoto, os microrganismos decompositores, por possuírem requisitos de sobrevivência mínimos, ganham a competição pelo uso do oxigênio dissolvido na água e satisfazem seus metabolismos. Assim, pode ocorrer uma falta de oxigênio para os outros grupos, os peixes, por exemplo, morrem e formam mais matéria orgânica em suspensão, ou deposição, e a população dos microrganismos cresce mais rapidamente - exigindo mais oxigênio para decomposições. Dessa forma, a matéria orgânica em excesso pode causar o que chamamos de poluição aquática, que é o fim do oxigênio dissolvido na água. A redução do oxigênio dissolvido pelo alto consumo dos decompositores prejudicam os seres produtores e consumidores. Isso coloca em risco todo o ecossistema aquático e o ser humano perde a salubridade desse ambiente.

O Oxigênio Dissolvido (OD) na água é um dos principais indicadores da qualidade desse ecossistema, pois sua demanda é requisitada por todos os seres vivos deste ambiente aquático. Essa Demanda Bioquímica de Oxigênio, (DBO), relaciona o organismo e a sua sobrevivência com o grau de poluição de um corpo hídrico. Ao avaliar a DBO de rios, riachos e lagos saberemos quais seres estarão vivos ou mortos. Por outro lado, quando o oxigênio dissolvido começa a ficar ausente, entram em cena outros microrganismos, os chamados anaeróbios. Esses decompositores não necessitam de oxigênio e liberam substâncias que conferem odor, sabor e aspectos indesejáveis à água. É o começo do fim de um ecossistema aquático. Peixes e outros seres vivos de um corpo hídrico necessitam uma concentração de oxigênio dissolvido entre 2mg/l e 4mg/l para existirem na forma de vida aeróbia superior.

A concentração de oxigênio dissolvido em rios e riachos depende de diversas variáveis, dentre algumas, temos:

• As características dos despejos de esgotos dos diversos setores da sociedade, tais como a concentração de resíduos suspensos nos efluentes de esgotos domésticos, industriais e comerciais que podem conter misturas não biodegradáveis, tais como, detergentes, produtos de higiene, produtos farmacêuticos entre outros;
• As características dos corpos d’águas associadas à facilidade com que as cargas poluidoras são misturadas neste meio, tais como a velocidade do fluido, a geometria do canal de escoamento, inclinação do canal, difusão turbulenta etc.;
• A produção de oxigênio dissolvido que pode ser originada pela produção de fotossíntese dos organismos produtores e pela reaeração, que é a passagem do oxigênio atmosférico para dentro do corpo d’água (interface ar-água).

Um corpo hídrico poluído por lançamento de matéria orgânica biodegradável, ou não, pode sofrer um processo natural de recuperação chamado de autodepuração. Este fenômeno acontece por meio de processos físicos, como diluição e sedimentação; químicos, como oxidação e biológicos, como decomposições dos microrganismos aeróbios.

Em rios e lagos podem ocorrer excessos dos nutrientes. Grande quantidade de nutriente ocasiona o crescimento exagerado das algas. Esse processo é chamado de eutrofização. Embora a geração de algas seja necessária para dar suporte à cadeia alimentar, a sua proliferação excessiva acarreta a deterioração do corpo hídrico. Porém, os rios são raramente eutrofizados por possuírem águas correntes. A principal diferença entre um rio e um lago é que o primeiro é continuamente "lavado" pelas águas. Com relação ao fluxo da água, os rios e riachos são chamados de ecossistemas lóticos. Lagos e tanques, que não possuem águas correntes, ou até mesmo um riacho com fluxo muito lento, são chamados de ecossistemas lênticos.

No infográfico da Figura 1, as regiões anterior e posterior ao lançamento de matéria orgânica biodegradável por um efluente estão associadas aos gráficos da concentração de OD e da DBO por tempo, ou distância percorrida pela pluma de poluentes desde a fonte poluidora. Nesse gráfico é possível observar a evolução das linhas que indicam o OD e a DBO por zonas de impactos à jusante.

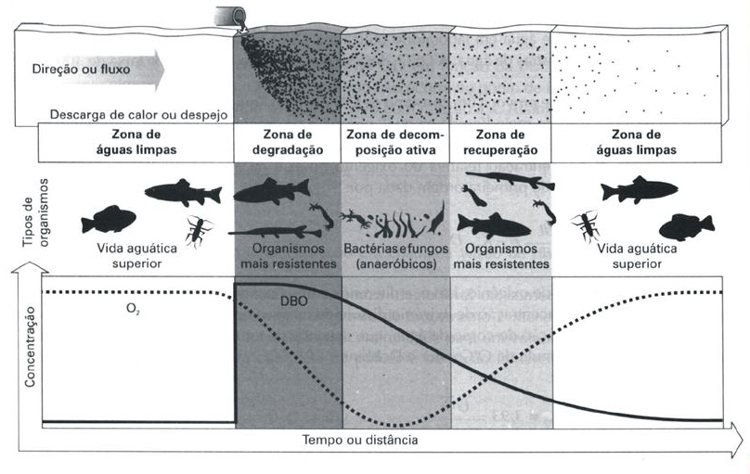
Figura 1 Fonte: Braga e outros. Introdução à Engenharia Ambiental. 2ª ed. São Paulo: Pearson, 2005.

As águas correntes de um rio podem ser caracterizadas, hidraulicamente, como um reator de fluxo, tipo um pistão, como alusão ao instrumento musical de sopro. Esta estratégia de análise permite utilizar o Cálculo Diferencial e Integral para aferir a taxa de crescimento, ou decrescimento, do oxigênio dissolvido, ou seja, o potencial poluidor do efluente através da propagação da pluma de esgoto que se desloca misturada com a correnteza do rio. Essa pluma caminha à jusante dependendo de fatores como o tempo e a velocidade do fluxo da correnteza (figura 2).

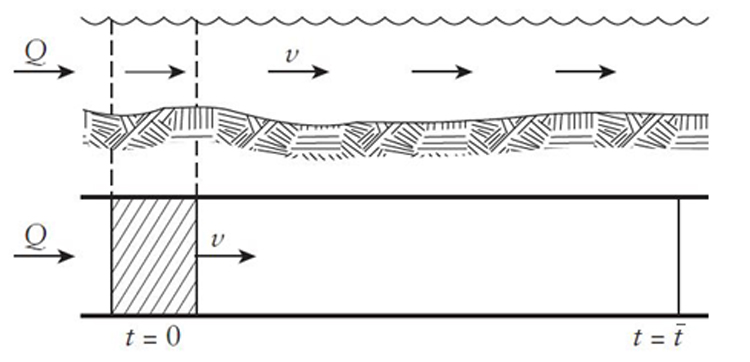
Figura 2 Fonte: Vesilind e Morgan. Introdução à Engenharia Ambiental. 2ª ed. São Paulo: Cengage Learning, 2014.

Se considerarmos que neste reator o fluxo (pistão) realiza uma reação, taxa de variação do poluente com o tempo, de primeira ordem, a matéria orgânica biodegradável despejada reagirá com a água. Assim, a taxa de reação \( A \), que caracteriza o consumo ou destruição do oxigênio utilizado pelos organismos decompositores, pode ser expressa como:

\begin{equation} \frac{dA}{dt}=-kA \end{equation}

A equação 1 pode ser integrada entre \( A_{0} \) e \( A \), na variação temporal entre \( t_{0} \) e \( t \), após separação das variáveis, assim:

\[ \int_{A_{0}}^{A}\frac{dA}{A}=-k\int_{t_{0}}^{t}dt \] \[ lnA-lnA_{0}=-kt \] \[ ln\frac{A}{A_{0}}=-kt \] \[ \frac{A}{A_{0}}=e ^{^{-kt}} \] \begin{equation} {A}={A_{0}}\cdot e ^{^{-kt}} \end{equation}

Onde,

A = quantidade qualquer de nutriente, normalmente necromassa,

A₀ = quantidade qualquer logo após o lançamento,

dA/dt = taxa de reação,

k = constante da taxa de reação,

t = tempo.

A Equação 2, que é a solução da integração, mostra que esta variação é exponencial com sinal negativo, ou seja, a taxa de degradação diminuirá com o passar do tempo. Num ecossistema aquático as reações causadas durante o fluxo do pistão não param de ocorrer. Além da reação de primeira ordem ocorrem reações de segunda ordem e outras sucessivamente. Numa segunda reação, ou seja, a reação de segunda ordem, pode ser expressa como:

\begin{equation} \frac{dA}{dt}=-kA^{2} \end{equation} \[ \int_{A_{0}}^{A}\frac{dA}{A^{2}}=-k\int_{t_{0}}^{t}dt \] \[ -\frac{1}{A}+\frac{1}{A_{0}} = - kt \] \[ \frac{1}{A}-\frac{1}{A_{0}} = kt \] \[ \frac{1}{A} = \frac{1}{A_{0}} + kt \] \[ \frac{1}{A} = \frac{1 + {A_{0}}\cdot kt}{A_{0}} \] \begin{equation} A=\frac{A_{0}}{1 + {A_{0}}\cdot kt} \end{equation}

As reações podem ser consecutivas envolvendo diversos materiais. A equação 1, que foi de primeira ordem para um material poluente com taxa de degradação A, evoluiu para um resultado com variação exponencial negativa (decrescimento do poluente ao longo da correnteza), que foi a equação 2. A equação 3 foi de segunda ordem e evoluiu para um resultado mais complexo, que foi a equação 4.

Numa situação mais real, com multiplos materiais, além de um poluente reagindo com a água, podemos ter uma segunda reação de primeira ordem com relação a uma outra taxa de degradação (outro poluente), que podemos chamar de B, a reação geral será:

\begin{equation} \frac{dB}{dt}=k_{1}A-k_{2}B \end{equation}

Onde,

k₁ e k₂ são constantes das taxas de reações das concentrações dos poluentes A e B, que saem do efluente e se misturam na água limpa formando plumas misturadas que se movimentam no sentido da corrente, e diluem-se à jusante, dependendo do volume de água do rio e da quantidade de poluente.

Observa-se na equação 5 que a concentração de A está sendo formada a uma taxa k₁A, por isso é positiva, enquanto a outra está sendo destruída a uma taxa k₂B, por isso é negativa.

Para obter o valor de B na equação 5 devemos integrar a expressão dB/dt, que fica como exercício de cálculo para o leitor. Esta integração é importante para determinar o grau de poluição de um rio. O resultado da integração produz a equação:

\begin{equation} B=\frac{k_{1}\cdot A_{0}}{k_{2}- k_{1}}\left ( e^{-k_{1}t}-e^{-k_{2}t} \right )+B_{0}\cdot e^{-k_{2}t} \end{equation}

A equação 6 foi utilizada pela primeira vez por Streeter e Phelps para elaborar um modelo matemático que mensura a taxa de oxigênio dissolvido em um riacho. O déficit de oxigênio dissolvido é B e aumenta com o resultado do consumo de oxigênio pelos microrganismos decompositores, mas existe uma entrada (reposição) de oxigênio na água a partir da atmosfera e, também, da fotossíntese. Estas reposições também contribuem como provedoras da autodepuração do rio.

Este modelo foi proposto inicialmente em 1925 por Harold Warner Streeter e Earle Bernard Phelps (1876-1953) a partir de um estudo do processo de reoxigenação e desoxigenação no Río Ohio, nos Estados Unidos, com base em dados obtidos desde maio de 1914 a abril de 1915.

Com este modelo pode-se entender que quando um rio recebe efluente de matéria orgânica biodegradável a ação simultânea de reoxigenação e desoxigenação formam o que se denomina curva do oxigênio dissolvido (Figura 3), que será detalhado na próximo seção.

Figura 3 Fonte: Vesilind e Morgan. Introdução à Engenharia Ambiental. 2ª ed. São Paulo: Cengage Learning, 2014.

3 Modelo de Streeter-Phelps

O modelo de Streeter-Phelps é um modelo matemático que possibilita avaliar o mecanismo que define a taxa de variação do oxigênio dissolvido em um corpo hídrico quando recebe a descarga de águas residuais, com decomposição de matéria orgânica, e a aeração (reposição) de oxigênio por fotossíntese e por penetração do oxigênio atmosférico. Este modelo tem sido adaptado tanto para fontes pontuais como para fontes difusas ou dispersas de poluentes.

A Figura 3 apresenta a forma da curva do oxigênio dissolvido como resultado da soma da taxa de consumo do oxigênio pelos organismos, que é a desoxigenação, e a taxa de fornecimento por fotossíntese e por penetração atmosférica através da interface ar-água, que é a reoxigenação. Se a taxa de utilização for grande, como no trecho logo após a descarga da matéria orgânica biodegradável, (compare a Figura 1 com a Figura 3), o nível de oxigênio dissolvido cai porque a taxa de fornecimento não pode acompanhar o uso de oxigênio pelos decompositores, e cria um déficit. O Déficit (\( D \)) é definido como a diferença entre a quantidade máxima de oxigênio que a água limpa poderia conter, ou seja, a Saturação (\( S \)), e a concentração (\( C \)) de oxigênio dissolvido na água do rio, assim:

\begin{equation} D = S - C \end{equation}

Onde,

D = déficit de oxigênio, mg/l,

S = nível de saturação de oxigênio na água (o máximo de oxigênio que pode conter), mg/l,

C = concentração de oxigênio dissolvido na água, mg/l

Na Figura 3 pode-se observar que após a alta taxa inicial de decomposição, quando a matéria orgânica é decomposta pelos microrganismos decompositores, a taxa de utilização de oxigênio diminui porque os materiais que menos se decompõem permanecem. Com o uso de tanto oxigênio, o déficit é grande, mas o fornecimento de oxigênio da atmosfera é alto e começa acompanhar a utilização, que é uma situação favorável para a autodepuração. Portanto, o déficit começa a ser reduzido e, mais uma vez, atinge os níveis de saturação. Quando o déficit aumenta começa a poluição.

Este processo foi analisado por Streeter e Phelps e descrito em termos de reações consecutivas, como a equação 5. A taxa de utilização do oxigênio e a taxa de reabastecimento de oxigênio foram expressas, na notação de Streeter e Phelps, da seguinte forma:

\begin{equation} \frac{dD}{dt}=k_{1}z-k_{2}D \end{equation}

Onde,

z é a quantidade de oxigênio necessária para os microrganismos que estão decompondo a matéria orgânica. \( k_{1} \) é a constante de desoxigenação e \( k_{2} \) é a constante de reoxigenação, D é o déficit da concentração de oxigênio.

A taxa de variação do Déficit \( D \) depende da concentração de matéria orgânica a ser decomposta, ou da necessidade restante de oxigênio para os microrganismos \( z \) . Pode-se entender o Déficit em qualquer tempo \( t \). Considerando \( z \) como a taxa proporcional de oxigênio para ocorrer a decomposição em uma reação inicial de primeira ordem, podemos expressá-la por:

\begin{equation} \frac{dz}{dt}=-kz \end{equation} \[ \int_{z_{0}}^{z_{1}}\frac{dz}{z}=-k\int_{t_{0}}^{t}dt \] \[ lnz-lnz_{0}=-kt \] \[ ln\frac{z}{z_{0}}=-kt \] \[ \frac{z}{z_{0}}=e ^{^{-kt}} \] \begin{equation} z=z_{0}e ^{^{-kt}} \end{equation}

Se \( z \) é a quantidade de oxigênio em qualquer tempo \( t \), e \( z_{0} \) é a demanda bioquímica de oxigênio final e, trocando a letra desta variável, fazendo \( z_{0} = L \) na equação 10, e substituindo o novo valor de \( z \) na equação 8, e após esta troca integrar a equação 8, que fica como exercício, o resultado será:

\begin{equation} D=\frac{k_{1}\cdot L_{0}}{k_{2}- k_{1}}\left ( e^{-k_{1}t}-e^{-k_{2}t} \right )+D_{0}\cdot e^{-k_{2}t} \end{equation}

Essa é a chamada equação de Déficit de Streeter-Phelps.

Onde,

D = déficit de oxigênio em qualquer tempo t, mg/l,

D₀ = déficit de oxigênio imediatamente abaixo da localização do efluente de poluentes, mg/l,

L₀ = demanda final de oxigênio imediatamente abaixo da localização do efluente do poluente.

A maior preocupação quanto à qualidade da água é com o ponto na corrente aquática em que o déficit é maior, ou seja, onde a concentração do oxigênio dissolvido é mínima. Essa análise pode ser utilizada para estabelecer o grau de poluição de um rio ou riacho. Inclusive, pode ser utilizada para saber o grau de eficiência dos despejos dos efluentes das Estações de Tratamento de Esgoto, ETE.

Sabe-se, por observação direta, que não adianta o tratamento do esgoto por uma ETE se o despejo após a água residual ser tratada é num rio que está com sua biota morta. O rio precisa ser tratado antes, para depois analisar se a carga do efluente será diluída pelas águas correntes (autodepuração) ainda dentro do trecho municipal contemplado pelo saneamento. Assim, evitará morte do ecossistema, que chamamos de poluição. Caso aconteçam despejos num rio já morto, os gestores públicos contribuirão com amplificações para a destruição do sistema hidrológico dessa região.

Não adianta sanear uma rua se os moradoras do bairro não foram avisados e nem foram promovidas ações de educação ambiental pelo poder público local. Os moradores deverão entender que seus esgotos serão conectados aos troncos-coletores que passarão em suas portas, para que assim não façam mais conexões clandestinas para sumidouros ou riachos que passam perto de suas casas. Esse fato é muito comum em comunidades na Baixada Fluminense, no Rio de Janeiro, e em outras periferias de centros urbanos. As pessoas devem participar das ações do governo sobre a construção de uma ETE no seu bairro e receberem incentivos (materiais, mão-de-obra etc.) para conectarem seus efluentes aos novos troncos coletores instalados, pois na maioria dos casos essas obras acontecem em bairros cujas pessoas são mais desfavorecidas e sozinhas não teriam condições de arcar com as despesas para conectar com tubulações os seus lares ao novo sistema de saneamento instalados pelo poder público.

Além disso, a equação 11, de Streeter-Phelps, permite também avaliar em que condições as espécies (biota) ficariam vivas nos rios ou riachos após despejos dos efluentes de esgotos. A existência de microrganismos nos rios e riachos qualifica sanitariamente a existência de seres vivos em ecossistemas, inclusive a do humano, pois todos os organismos vivos fazem parte da cadeia alimentar de todo o trecho urbano, ou rural, cortado por rios e riachos. Deve-se observar que todo corpo hídrico contribui com a cadeia alimentar de sua região. A rede hidrológica está associada com a saúde coletiva.

Se na equação 11 for definido dD/dt = 0, que é a condição de máximo e mínimo do Cálculo, pode ser realizado o processo matemático de integração e obter uma equação resultante que avalia o ponto em que a curva do oxigênio dissolvido chega ao mínimo e começa a subir (a integração fica como exercício). A equação resultante dessa integração permite avaliar este momento crítico de um rio à jusante, o resultado da integração será:

\begin{equation} t=\frac{1}{{}k_{2}-k_{1}}\cdot ln\left [\frac{k_{2}}{k_{1}}\left (1-\frac{D_{0}\left ( k_{2}-k_{1} \right )}{k_{1}\cdot L_{0}} \right ) \right ] \end{equation}

4 Balanço de massa e vazão

Seria desejável, baseado no modelo de Streeter-Phelps, que a vazão da descarga do poluente pudesse ser muito pequena comparada com a vazão do rio. Porém, nem sempre isso acontece. O volume de descarga dos poluentes, na maioria das cidades brasileiras, não está permitindo autodepuração de seus rios urbanos. Mas se fosse verdadeiro, o primeiro ponto limpo no rio abaixo do ponto de descarga teria o mesmo déficit que no ponto antes da descarga do efluente, autodepuração perfeita. O balanço de cargas sobre o pistão no ponto de descarga do efluente, em t=0, na figura 3, apresenta uma mistura das vazões do rio e da descarga do poluente.

Ao comparar a figura 3 com a figura 4, abaixo, e denominarmos vazão como Q e concentração como C, observa-se que no ponto de descarga, ponto 0, a vazão da corrente de água do rio à montante e a sua concentração de oxigênio dissolvido à montante serão Q_M e C_M, respectivamente, e a vazão e a concentração de oxigênio dissolvido do efluente de poluição serão Q_P e C_P. À jusante, denominam-se a vazão como Q_J e a concentração como C_J, já misturadas.

Figura 4 Fonte: Vesilind e Morgan. Introdução à Engenharia Ambiental. 2ª ed. São Paulo: Cengage Learning, 2014.

Será necessário realizar um balanço de massa, como a conservação de energia, aplicando a Equação da Continuidade (Mecânica dos Fluidos ou Fenômenos de Transporte), para entender o que ocorre com as vazões diferenciadas do rio, do efluente e da vazão misturada de água limpa do rio com a do efluente, em um processo de diluição dos poluentes até uma autodepuração. Para isso, utilizaremos o conceito de caixa-preta, assim:

ENTRADA = SAÍDA

\begin{equation} Q_{M}+Q_{P}=Q_{J} \end{equation}

Em outras palavras, a concentração de oxigênio na vazão à jusante da fonte de poluição é uma combinação da concentração de oxigênio da vazão à montante da descarga e da concentração de oxigênio da vazão do efluente. Uma vez que o déficit é igual a \( D = S - C \), o déficit inicial \( D_{0} \) deve ser uma combinação do déficit na vazão à montante , \( D_{M} \), e do déficit do Poluente, \( D_{P} \).

Onde,

D = déficit de oxigênio em qualquer tempo t,

D₀ = déficit de oxigênio da vazão imediatamente abaixo da localização do efluente de poluentes,

D_M = déficit de oxigênio da vazão à montante,

D_S = déficit de saturação,

Q_M = fluxo à montante,

C_M = concentração de oxigênio à montante,

Q_P = fluxo da fonte poluidora,

C_P = concentração da fonte poluidora,

Q_J = fluxo à jusante,

C_J = concentração de oxigênio à jusante (mistura).

Antes de prosseguir com a interpretação do infográfico apresentado na figura 4, acima, deve-se esclarecer quais são as diferenças importantes no Brasil sobre o que é um fluxo, ou melhor, quando ele é vazão e quando ele é carga. Em Física Ambiental o fluxo pode ser gravimétrico (massa) ou volumétrico (volume). O primeiro se expressa em kg/s e o segundo em m³. No Brasil, o fluxo gravimétrico é chamado de carga e o fluxo volumétrico é chamado de vazão.

Esses fluxos são interdependentes. A massa de um material que passa por um trecho de um rio durante um intervalo de tempo se relaciona com o volume desse material pela equação:

\[ \rho=\frac{M}{V} \]

Onde,

ρ = massa específica, kg/m³,

M = massa, kg,

V = volume m³.

Assim, no Brasil, a vazão seria Q_volumétrico e a carga seria Q_mássico. A concentração pode ser definida como uma massa específica, do seguinte modo:

\[ C=\dfrac{Q_{m\acute{a}ssico}}{Q_{volum\acute{e}trico}} \]

Então,

\[ Q_{m\acute{a}ssico}=Q_{volum\acute{e}trico}\cdot C \]

Por isso chamamos de balanço de massa. As diferentes vazões na figura 4, ou seja, o balanço no ponto de despejo do poluente será um balanço em termos de vazão e concentração, que pode ser escrito como:

\[ Q_{M}C_{M}+ Q_{P}C_{P}=Q_{J}C_{J} \]

Se \( Q_{J} = Q_{M} + Q_{P} \) , temos para a concentração de oxigênio na mistura à jusante entre a água do rio e o efluente, a seguinte equação:

\begin{equation} C_{J}=\dfrac{Q_{M}C_{M}+ Q_{P}C_{P}}{Q_{M}+Q_{P}} \end{equation}

Observe que a equação 14 do balanço de massa indica que se a vazão do poluente chegar a ser zero, \( Q_{P} = 0 \), a concentração de oxigênio à jusante será igual a concentração de oxigênio do rio antes do despejo do poluente (situação ideal).

Por outro lado, o nível de oxigênio dissolvido em água limpa corrente influencia e gera uma dependência com a temperatura da água nos momentos antes e depois do despejo do poluente. Vários estudos são realizados para determinar esta dependência de forma empírica, ou seja, com medições realizadas nestes pontos. A tabela apresentada abaixo mostra a relação do oxigênio dissolvido com várias temperaturas.

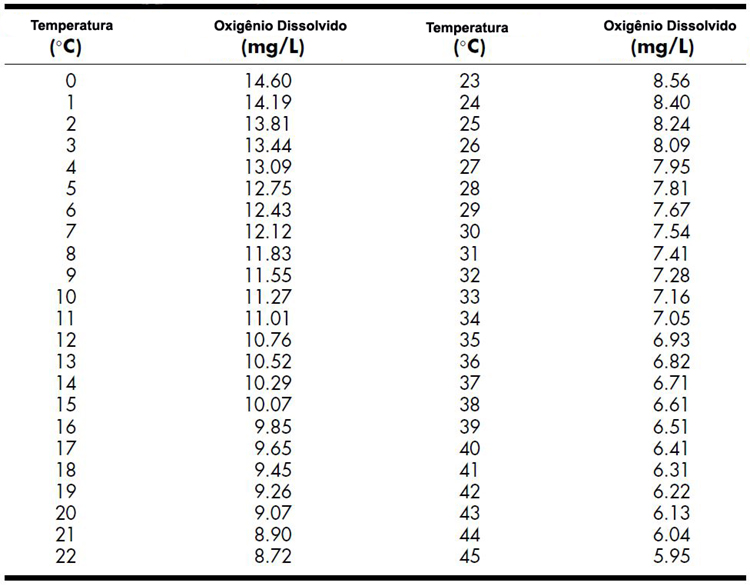
Figura 5 Fonte: Vesilind e Morgan. Introdução à Engenharia Ambiental. 2ª ed. São Paulo: Cengage Learning, 2014.

A tabela acima mostra que quanto mais "quente" for a água, menos seres vivos (microrganismos - flora e fauna) ela terá, pois diminui a concentração de oxigênio dissolvido. O aquecimento dos ecossistemas aquáticos é uma das preocupações com relação ao desequilíbrio climático global, porque esta crise ecológica faz aumentar a temperatura média do planeta e se soma com a degradação de rios e mares. Os despejos não controlados de efluentes também interfere na temperatura dos corpos hídricos amplificando a crise ambiental em curso.

Uma vez que a concentração de oxigênio dissolvido da mistura de água limpa com águas residuárias, depois do despejo, ou seja, à jusante, foi determinada conforme a equação 14, a temperatura da água da mistura à jusante pode ser calculada utilizando-se a seguinte equação:

\begin{equation} T_{J}=\dfrac{Q_{M}T_{M}+ Q_{P}T_{P}}{Q_{M}+Q_{P}} \end{equation}

O valor da saturação do oxigênio à jusante, \( S_{0} \) em um \( T_{0} \) , pode ser encontrada na Tabela acima. O déficit inicial é então calculado como:

D₀ = S₀ - C₀

Da mesma forma, o rio também pode ter uma Demanda de Oxigênio dissolvido, DBO, à jusante do ponto de despejo do efluente. Supondo que a mistura fique completa, a DBO à jusante deve ser calculada por:

\begin{equation} L_{J}=\dfrac{L_{M}Q_{M}+ L_{P}Q_{P}}{Q_{M}+Q_{P}} \end{equation}

Onde,

L_J = demanda final de oxigênio abaixo do despejo do efluente,

L_M = demanda final de oxigênio da água antes do despejo do efluente,

L_P = demanda final de oxigênio do poluente despejado.

Além disso, deve-se ressaltar que, uma importante fórmula popular generalizada para avaliar a constante de reoxigenação do modelo de Streeter-Phelps e suas relações com a temperatura da água, a velocidade do fluxo e a profundidade média de um canal, pode ser dada por:

\begin{equation} k_{2}=\dfrac{3,9.v^{1/2}.[1,025^{(T-20)}]^{1/2}}{H^{3/2}} \end{equation}

Onde,

T = temperatura da água, °C

v = velocidade média da corrente, m/s

H = profundidade média da vazão, m.

O termo correspondente à temperatura representa a variação da taxa da temperatura, os termos H e v descrevem a energia cinética no rio e a facilidade de transporte de oxigênio (O₂) em razão da profundidade da água. Um meio alternativo de obter os valores para k₂ é a utilização, segundo O'Connor e Dobbins, de 1958, dos seguintes valores empíricos para 20 °C/dias:

Onde,

pequenos córregos = 0,1 a 0,23

pequenos rios com baixa velocidade = 0,23 a 0,35

grande rios, velocidade lenta = 0,35 a 0,46

grande rios, velocidade normal = 0,46 a 0,69

rios muito rápidos = 0,69 a 1,15

corredeiras = 1,15.

5 Referências

1. VESILIND E MORGAN, P. Aarne. Introdução à Engenharia Ambiental. São Paulo: Editora Cengage Learnig, 2014.
2. MIHELCIC, James R. ; ZIMMERMAN, Julie B. Introdução à engenharia ambiental: fundamentos, sustentabilidade e projetos. Tradução Ramira Maria Siqueira da Silva. Rio de Janeiro: Editora LTC, 2018.
3. BRASIL. Ministério da Saúde. Fundação Nacional de Saúde. Manual de Saneamento / Ministério da Saúde, Fundação Nacional de Saúde. – 5. ed. – Brasília : Funasa, 2021.
4. BRAGA, Benetido et al. Introdução à engenharia ambiental: o desafio do desenvolvimento sustentável. 2ª ed. São Paulo: Pearson Prentice Hall, 2005.
5. VON SPERLING, Marcos. Introdução à qualidade das águas e ao tratamento de esgotos. 4ª ed. Belo Horizonte: Editora UFMG, 2014.